4.1. Comparaison de deux ou plusieurs distributions

Ce sont des tests d'homogénéité.

Le cas le plus simple consiste à comparer deux répartitions dont l'une est théorique, la variable qualitative étudiée étant répartie en deux classes (variable de type Bernouilli).

La situation est résumée dans le tableau suivant :

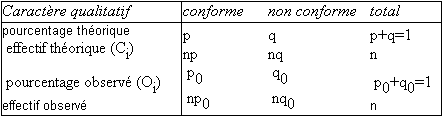
La méthode employée est basée sur la comparaison des effectifs observés et des effectifs théoriques (ou calculés) en utilisant la distribution du Khi deux.

On définit la fonction discriminante (variable Χ2 ) suivante :

X2=

On rappelle que les fluctuations d'échantillonnage de cette variable sont connues et qu'elles suivent la distribution théorique du Khi deux décrites dans le chapitre II.

Sous l'hypothèse H0 (p=p0), ce sont les fluctuations d'échantillonnage qui peuvent expliquer la différence mesurée entre les 2 pourcentages.

Pour vérifier ou infirmer cette hypothèse, on comparera donc la valeur de X2 calculée avec la valeur lue dans la table du Khi deux avec un risque α et un nombre de degrés de liberté égal à 1 (k-1 ddl où k est le nombre de classes de la distribution).

Si X2<Xα2 , on acceptera H0

Si X2>Xα2 ,on rejette H0 et on accepte H1, au risque α près.

Le test du Khi deux peut être généralisé à la comparaison de plusieurs distributions. Nous avons déjà donné un exemple dans le chapitre II concernant la comparaison de la distribution des points indiqués par les faces d'un dé au cours de 100 lancers avec la distribution théorique basée sur l'équiprobabilité de chaque faces.

La variable testée reste la même que précédemment :

X2=

Sous H0, elle est comparée à la valeur tabulée pour un risque α et k-1 ddl.

Si l'on accepte H0, on conclut que l'échantillon provient d'une population dont le caractère qualitatif est distribué avec les pourcentages théoriques (équiprobabilité p=1/6 dans l'exemple des lancers de dé).

Ce même test permet de comparer plusieurs distributions observées comme le montre l'exemple suivant portant sur un contrôle qualitatif des pièces usinées à l'aide de deux procédés différents :

Le problème revient à savoir si les répartitions observées avec les procédés A et B diffèrent significativement. En d'autres termes, on se demande si les deux échantillons proviennent d'une même population et si les écarts entre les nombres de défauts observés sont dus à des fluctuations d'échantillonnage.

Ce type de test est appelé test d'indépendance. On remarquera que les caractères étudiés (type de procédé et type de défauts) sont deux caractère qualitatifs et que l'on cherche ainsi à démontrer ou infirmer l'indépendance entre les deux caractères : le procédé influence ou non la qualité des pièces usinées.

Il est toujours important dans ce type de problème de savoir si les deux caractères étudiés sont aléatoires ou contrôlés. Dans cet exemple, seul le caractère « type de défaut » est aléatoire. En revanche le caractère «procédé » est un caractère contrôlé car c'est l'expérimentateur qui le détermine.

Notons également que dans cet exemple, les défauts de taille pourraient être analysés de façon quantitative (mesurés) ce qui modifierait complètement la méthode statistique utilisée pour résoudre le problème (on reviendrait au problème de comparaisons de moyennes pour vérifier si les tailles mesurées dans les deux échantillons diffèrent significativement).

L'analyse du problème posé dans notre exemple nécessite maintenant de déterminer des effectifs théoriques (ou calculés) correspondant à l'hypothèse H0 : indépendance entre les deux caractères.

L'hypothèse alternative H1 est : dépendance entre les deux caractères.

Ces effectifs seront calculés pour chaque cellule du tableau de contingence en utilisant la formule suivante : , où Tl est le total de la ligne, Tc le total de la colonne et TG le total général. On obtient le tableau suivant avec entre parenthèses les effectifs calculés :

On peut aussi exprimer la probabilité qu'une pièce produite avec le procédé A présente un défaut de couleur. Si les deux caractères sont indépendants, cette probabilité est p(procédé A et défaut de couleur)=p(procédé A) x p(défaut de couleur)= 116/244 x 35/244

Ramenée à l'effectif total, cette probabilité donne la valeur ci.

Dans l'hypothèse où il y a indépendance entre les deux caractères, la variable Khi deux donne :

X2= =8,31. Cette valeur est comparée à la valeur lue dans la table au risque 5 % avec (l-1)(c-1)=(2-1)(4-1)=3 degré de liberté (l et c représentent le nombre de lignes et de colonnes du tableau de contingence. Ici, on trouve X20,05=7,81.

X2>X20,05, on rejette H0. Il existe une relation entre le procédé de fabrication et la qualité des pièces produites (au risque 5%). Le degré de signification du test est de 4 %, probabilité correspondant à la valeur du X2 calculée (8,31).

Si l'expérimentation a été bien menée, c'est-à-dire que l'on a éliminé, en utilisant un protocole adapté, toutes les causes extérieures de variabilité en dehors du type de procédé (expérimentateur, tirage au sort des pièces...), on peut conclure à un lien de causalité entre le type de procédé et l'apparition de défauts : l'apparition de défaut est due au procédé et n'est pas accidentelle, due au hasard. La conclusion du test est que dans l'ensemble, l'apparition de défauts est liée au procédé.

Ce lien de causalité ne peut être établi, dans une étude statistique, que si l'un des caractères qualitatifs est contrôlé et qu'il y a eu tirage au sort pour l'obtention des échantillons. On parle d'étude statistique de type expérimentale.

Le deuxième exemple représente l'analyse de la répartition de deux caractères qualitatifs purement aléatoires :

• couleur des cheveux

• couleur des yeux

On cherche à savoir s'il existe une relation entre ces deux caractères. On peut obtenir une information en répertoriant ces deux caractères dans un échantillon représentatif.

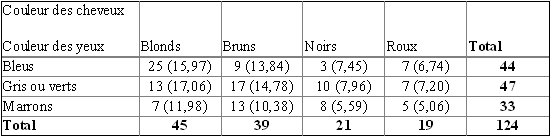
Les effectifs théoriques (nombres entre parenthèses) sont calculés en considérant que les deux caractères sont indépendants (hypothèse H0).

La valeur du X2= est 15,06. Cette valeur est comparée à la valeur lue dans la table au risque 5 % avec (l-1)(c-1)=(3-1)(4-1)=6 degré de liberté. Ici, on trouve X20,05= 12,6.

X2>X20,05, on rejette H0. Il existe une relation entre la couleur des yeux et la couleur des cheveux (au risque 5%). Le degré de signification du test est de 2 %, probabilité correspondant à la valeur du X2 calculée (15,06).

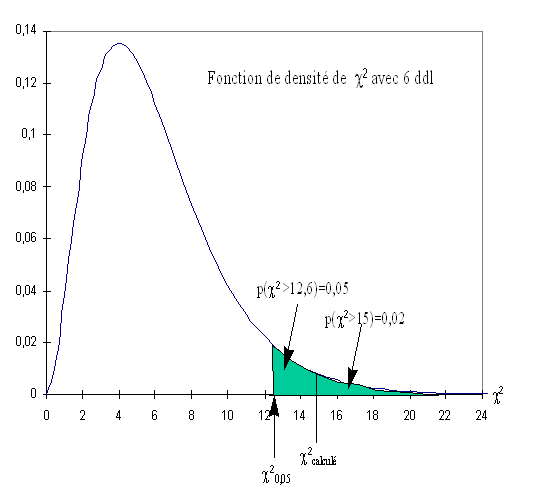
Contrairement à l'exemple précédent, on ne peut conclure ici à un lien de causalité entre les deux caractères qualitatifs, ceux ci étant purement aléatoire. On parlera ici d'enquête d'observation.